Hakkında uzun uzun konuşmak istediğim Polar Code makalemi tamamlamış olmanın verdiği mutluluğu sizlerle paylaşmak istiyorum. Bu konu, okurken, araştırırken, anlamaya çalışırken ve yazarken bana en çok keyif veren çalışmalardan biri oldu.
Giriş
Evrenin en temel yasalarından biri, bilginin bir bedeli olmasıdır. İletişim teorisinin kutsal metni sayılan Claude Shannon'ın 1948 tarihli çalışmasından bu yana tüm mühendislik çabaları, bir kanalın gürültünün boğduğu bir ortamda hatasız iletilebilecek maksimum veri hızını işaret eden Shannon Kapasitesi'ne ulaşmayı hedeflemiştir.
2009 yılında bu çıkmazı Türk bilim insanı Prof. Dr. Erdal Arıkan tarafından tanımlanan Polar Kodlar ile kırıldı. Arıkan, klasik kanal kodlama paradigmasının ötesine geçerek, kanal transformasyonu fikrini ortaya koydu. Bu yaklaşımda, bağımsız ve simetrik ikili girişli kanallar, kanal kapasitesine "polarize" edilmiş alt kanallara dönüştürüldü.
Kanal Polarizasyonu
Polar kodlamanın kalbindeki Kanal Polarizasyonu süreci, iletişim mühendisliği alanında temel bir paradigma değişikliğidir ve bunu anlamak için soyut bir fizik analojisine ihtiyacımız var. Bu süreci tıpkı termodinamikteki bir faz ayrışımı gibi düşünebiliriz. Başlangıçta homojen, ortalama bir kanalda gürültü ve belirsizlik (entropi) her yere eşit dağılmıştır. Polarizasyon ise, dışarıdan uygulanan bir kuvvet gibi, bu homojen yapıyı uç noktalara doğru iter ve kanalları ayrıştırır.
Bu kanalların \( K \) adeti, kapasiteleri 1'e yakınsayan, neredeyse kusursuz hâline gelirken; geriye kalan \( N - K \) adedi, kapasiteleri 0'a yakınsayan, tamamen kullanılamaz olarak kalır. Bu, kodlayıcının bilgi bitlerini stratejik olarak en güvenilir \( K \) adet kanala yerleştirmesini sağlar. Kalan \( N - K \) adet güvenilmez kanal ise, donmuş bitler (frozen bits) olarak adlandırılır ve genellikle sıfır olarak sabitlenir.
Binary Erasure Channel - BEC
Bu fiziksel ayrışımı matematiksel düzleme taşımak için, en basit hata modeli olan İkili Silme Kanalı (Binary Erasure Channel - BEC) üzerinde Arıkan'ın dehasını inceleyelim. BEC, \( p \) olasılığıyla bitin silindiği \( (Y=?) \) ve \( 1−p \) olasılığıyla hatasız iletildiği bir kanaldır.
İki özdeş kanalı, \( U_1 \) ve \( U_2 \) girişlerini kullanarak basit bir ağ ile birleştiriyoruz: \( X_1 = U_1 \oplus U_2 \) ve \( X_2 = U_2 \). Bu işlem, iki yeni sanal kanalı ortaya çıkarır: \( W^- \) (kötüleşen kanal) ve \( W^+ \) (iyileşen kanal).
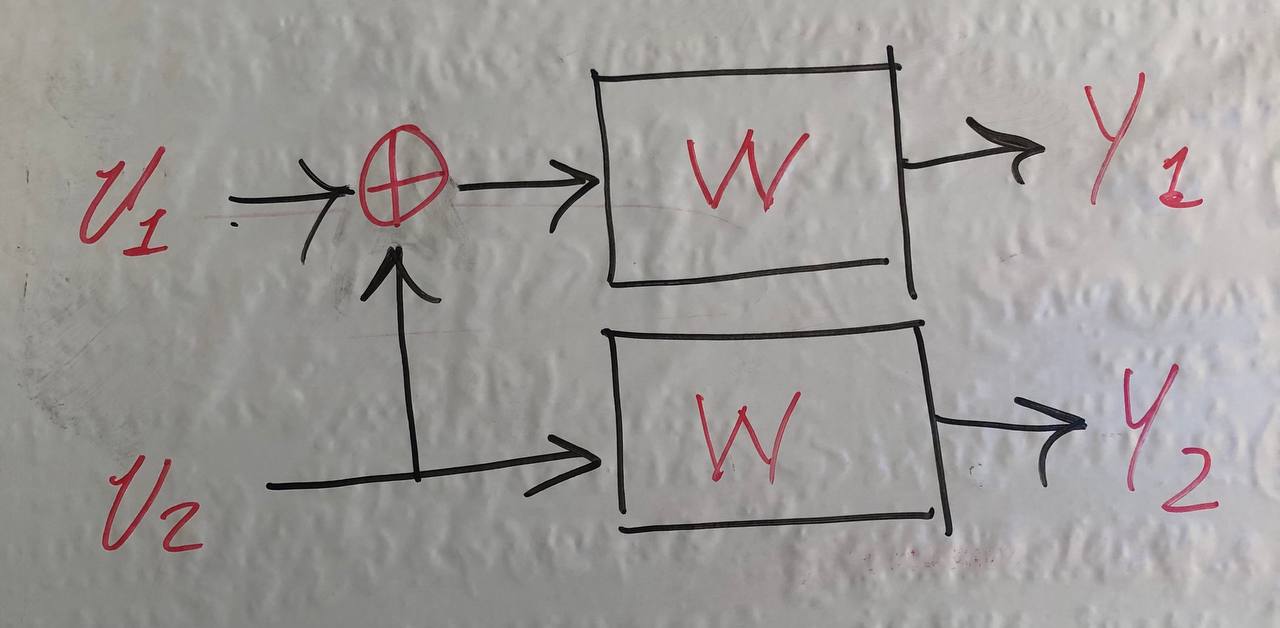
- \( W^- \) Kanalı: \( U_1 \rightarrow (Y_1, Y_2) \) dönüşümüne odaklanır. \( U_1 \)'in çözülebilmesi, ancak hem \( U_1 \oplus U_2 \) hem de \( U_2 \)'nin başarılı bir şekilde alındığı tek durumda mümkündür.
Başlangıçtaki \( p \) silme olasılığı, bu kanalda \( 2p - p^2 \) gibi daha yüksek bir değere çıkar. Bu kanal, orijinal BEC'den kesinlikle daha kötüdür.
\( W^+ \) Kanalı: \( U_2 \rightarrow (Y_1, Y_2, U_1) \) dönüşümüne odaklanır. Buradaki anahtar, \( U_1 \)'in tahmini değeri \( U_1 \)'in biliniyor varsayılmasıdır (Ardışık İptal Çözme prensibi). Bu bilgi, \( Y_1 \) alınamasa bile \( Y_2 \) alınırsa veya tam tersi, \( U_2 \)'nin çıkarılmasını büyük ölçüde garanti eder.
Başlangıçtaki \( p \) silme olasılığı, bu kanalda \( p^2 \) gibi daha düşük bir değere iner.
Somut Deney
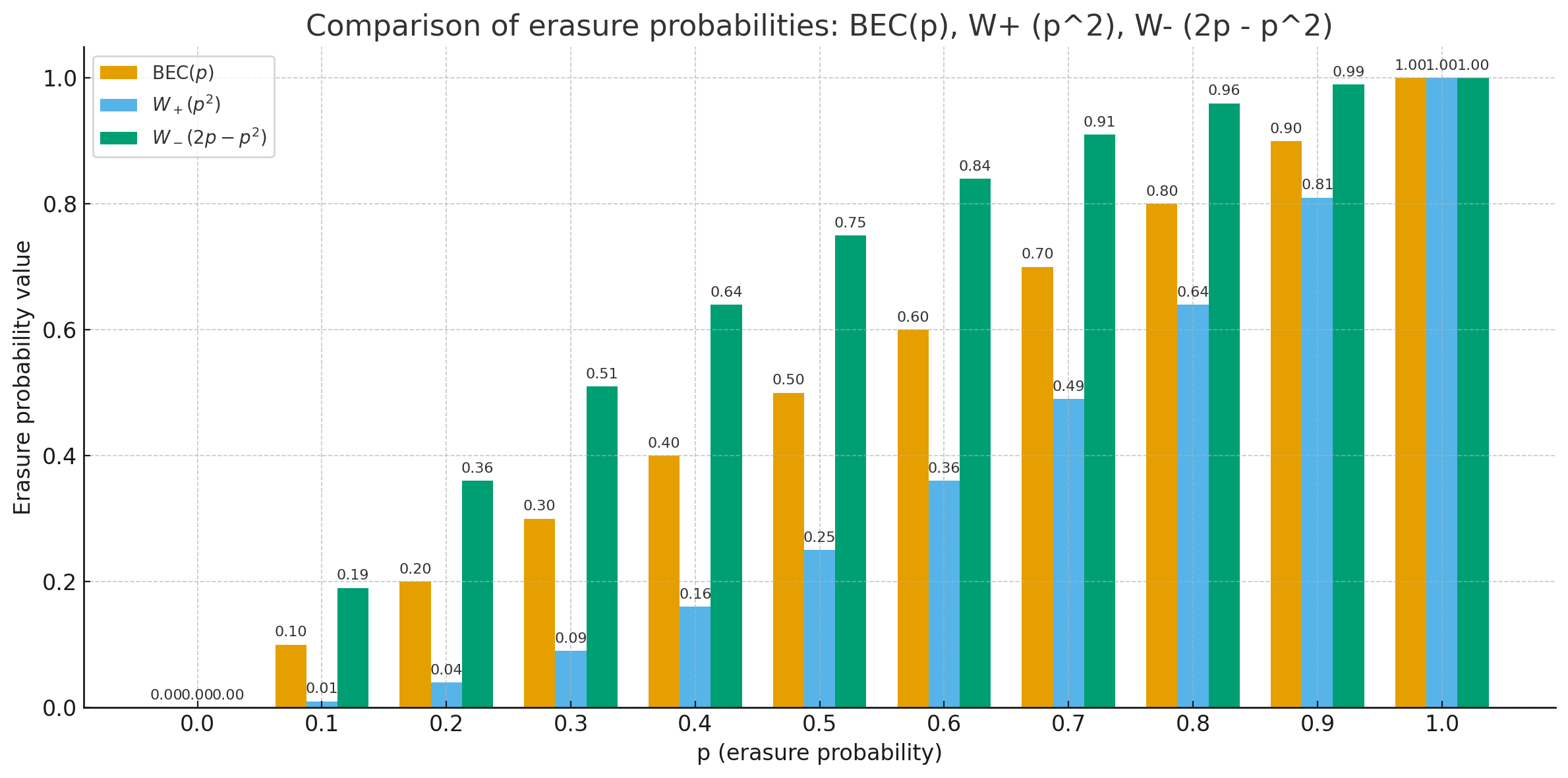
\( p = 0.3 \) silme olasılığıyla başladığımızda, tek bir polarizasyon adımında kanallarımız şuna dönüşür:
- \( W^- \): Silme olasılığı \( 0.51 \). (Kullanılamaz.)
- \( W^+ \): Silme olasılığı \( 0.09 \). (Mükemmele yakın.)
Özyinelemeli Polarizasyon
Bu basit iki kanallı dönüşüm, ortalama bir kanalı, kapasiteleri uç noktalara doğru itilmiş iki kanala ayırarak polarizasyonun temelini kanıtlar. Polar kodların gücü, bu \( 2 \times 2 \) dönüşümünün bir kez değil, \( n = \log_2 N \) kez özyinelemeli (recursive) olarak tekrarlanmasından gelir. Bu tekrarlama süreci, tüm kanalların kapasitelerini sıfıra veya bire yakınsatan bir fraktal yapı oluşturur.
Polar kodların sunduğu bu ikili takdir – kanalların kesinlikle saf "iyi" ve kesinlikle saf "kötü" olarak ayrılması tıpkı antik mitlerdeki iki yüzlü tanrıların veya kaçınılmaz kaderin tecellisi gibi bir analoji kurduruyor.
Felsefi Yorum: Yin ve Yang
Belki de en çok Yin ve Yang felsefesinin saf bir iletişim teorisi yorumudur. Yin ve Yang, evrendeki her şeyin karşıt, ancak birbirini tamamlayan güçlerle var olduğunu öğretir. Polar kodlamadan önce, iletişim kanalı bir Gri Alan idi; ne tam olarak güvenilir ne de tamamen güvenilmez. Gürültü, hem \( W^+ \) hem de \( W^- \) potansiyelini aynı anda barındıran, kaotik bir T'ai Chi gibiydi.

Arıkan'ın dönüşümü, bu kaosu dağıtarak net bir Kutupluluk getirdi: \( W^- \) kanalı, tüm belirsizliği, kargaşayı ve entropiyi üzerine çeken Yin'in karanlık, dipsiz çukuruna dönüştü. \( W^+ \) kanalı ise, tüm bilgiyi, düzeni ve güvenilirliği toplayarak parlayan, saf Yang zirvesine ulaştı.
Saygılarımla...
Kaynaklar
- Arıkan, E. (2009). Channel Polarization: A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input Memoryless Channels. IEEE Transactions on Information Theory, 55(7), 3051-3073.
- Arıkan, E. (2009). On the Origin of Polar Coding. IEEE Information Theory Workshop.
